Safety in the Face of Adversity: Achieving Zero Constraint Violation in Online Learning with Slowly Changing Constraints

We present the first theoretical guarantees for zero constraint violation in Online Convex Optimization (OCO) across all rounds, addressing dynamic constraint changes. Unlike existing approaches in constrained OCO, which allow for occasional safety breaches, we provide the first approach for maintaining strict safety under the assumption of gradually evolving constraints, namely the constraints change at most by a small amount between consecutive rounds. This is achieved through a primal-dual approach and Online Gradient Ascent in the dual space. We show that employing a dichotomous learning rate enables ensuring both safety, via zero constraint violation, and sublinear regret. Our framework marks a departure from previous work by providing the first provable guarantees for maintaining absolute safety in the face of changing constraints in OCO.

Log Barriers for Safe Black-box Optimization with Application to Safe Reinforcement Learning

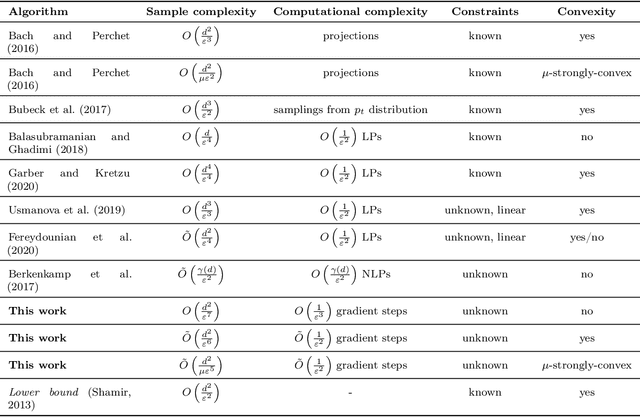
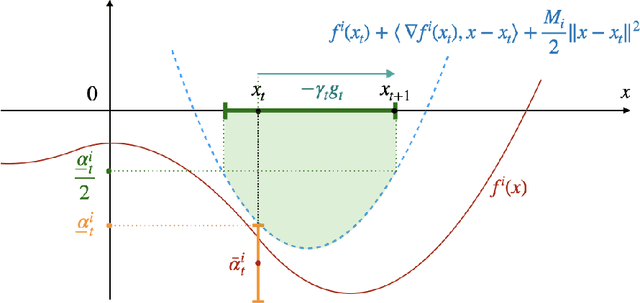
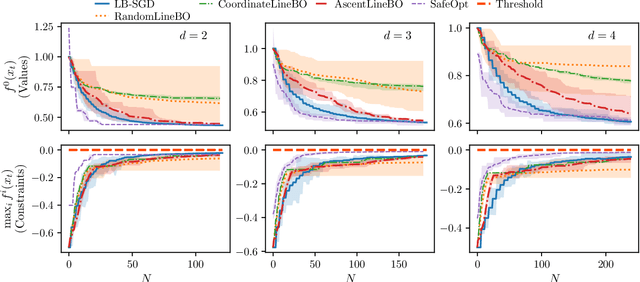
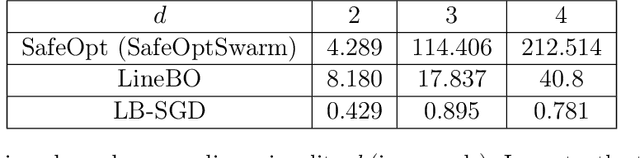
Optimizing noisy functions online, when evaluating the objective requires experiments on a deployed system, is a crucial task arising in manufacturing, robotics and many others. Often, constraints on safe inputs are unknown ahead of time, and we only obtain noisy information, indicating how close we are to violating the constraints. Yet, safety must be guaranteed at all times, not only for the final output of the algorithm. We introduce a general approach for seeking a stationary point in high dimensional non-linear stochastic optimization problems in which maintaining safety during learning is crucial. Our approach called LB-SGD is based on applying stochastic gradient descent (SGD) with a carefully chosen adaptive step size to a logarithmic barrier approximation of the original problem. We provide a complete convergence analysis of non-convex, convex, and strongly-convex smooth constrained problems, with first-order and zeroth-order feedback. Our approach yields efficient updates and scales better with dimensionality compared to existing approaches. We empirically compare the sample complexity and the computational cost of our method with existing safe learning approaches. Beyond synthetic benchmarks, we demonstrate the effectiveness of our approach on minimizing constraint violation in policy search tasks in safe reinforcement learning (RL).

Constrained Policy Optimization via Bayesian World Models

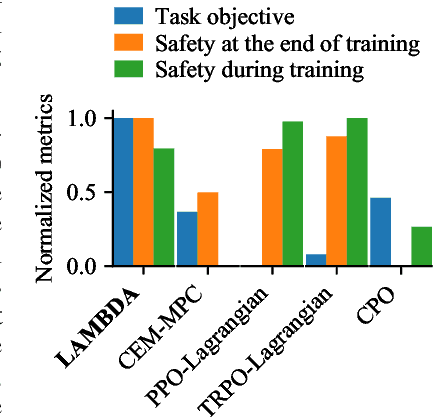
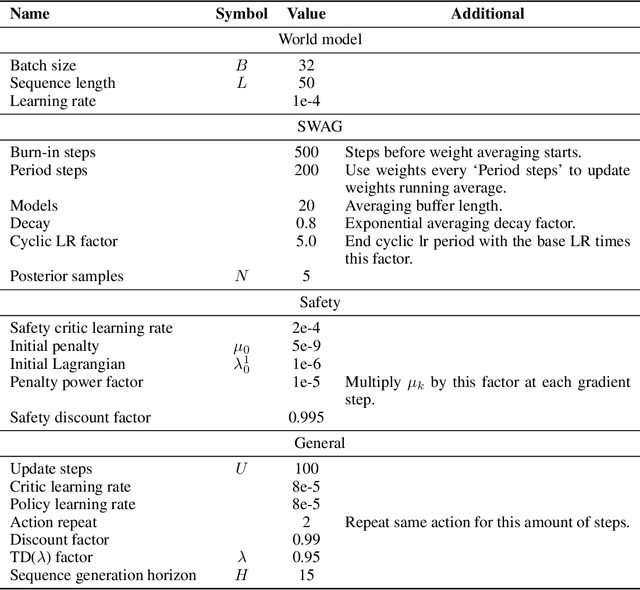
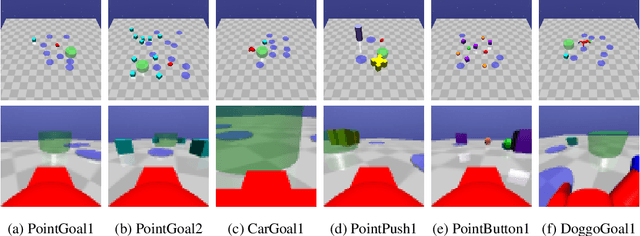
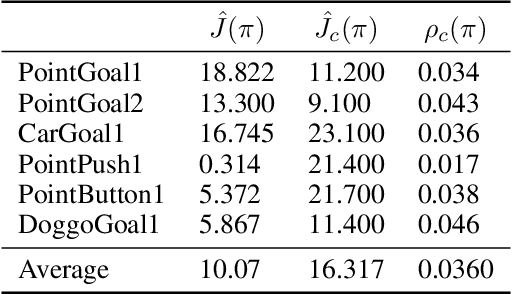
Improving sample-efficiency and safety are crucial challenges when deploying reinforcement learning in high-stakes real world applications. We propose LAMBDA, a novel model-based approach for policy optimization in safety critical tasks modeled via constrained Markov decision processes. Our approach utilizes Bayesian world models, and harnesses the resulting uncertainty to maximize optimistic upper bounds on the task objective, as well as pessimistic upper bounds on the safety constraints. We demonstrate LAMBDA's state of the art performance on the Safety-Gym benchmark suite in terms of sample efficiency and constraint violation.

Risk-averse Heteroscedastic Bayesian Optimization

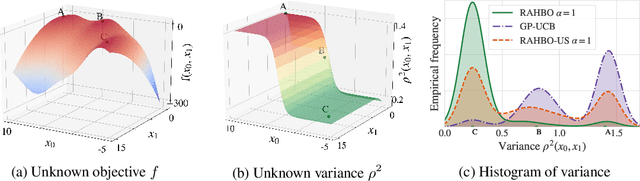
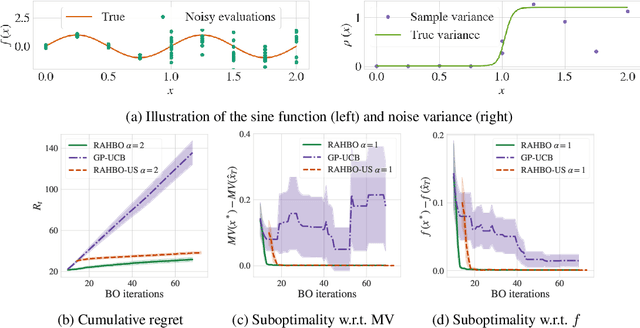
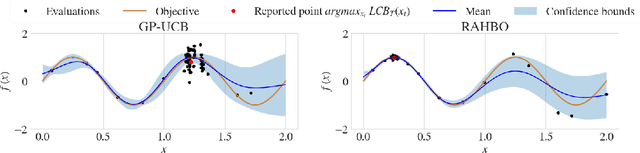
Many black-box optimization tasks arising in high-stakes applications require risk-averse decisions. The standard Bayesian optimization (BO) paradigm, however, optimizes the expected value only. We generalize BO to trade mean and input-dependent variance of the objective, both of which we assume to be unknown a priori. In particular, we propose a novel risk-averse heteroscedastic Bayesian optimization algorithm (RAHBO) that aims to identify a solution with high return and low noise variance, while learning the noise distribution on the fly. To this end, we model both expectation and variance as (unknown) RKHS functions, and propose a novel risk-aware acquisition function. We bound the regret for our approach and provide a robust rule to report the final decision point for applications where only a single solution must be identified. We demonstrate the effectiveness of RAHBO on synthetic benchmark functions and hyperparameter tuning tasks.